strIPlib Image Comparison (SIC)
ICIP is first introduced in the companion paper for this project, "An Image-based Approach to Detecting Structural Similarity Among Mixed Integer Programs." While this paper is under review, a draft has been made available on SSRN.
The purpose of this project was to demonstrate the types of insights which may be garnered by using ICIP. These insights are demonstrated through two separate analyses, the results of which are housed in this project directory (if you wish to jump straight to the second analysis included in this study, simply click here). For a discussion on the results housed on this page, please refer to the paper.
The first analysis in this project considers a subset of instances from the library of structured integer programs (strIPlib). These instances come from “pure” problems (e.g., the bin packing problem, the cutting stock problem), which are known to have clear and exploitable structures (namely for the application of column generation and other decomposition techniques). The relationships between some of these pure problems are known a priori. These relationships provide a “ground truth,” and allow for ICIP's performance to be validated. Note that several problem types include instances from more than one submission source - the results of this analysis are nested first by problem, then by source, and finally by instance.
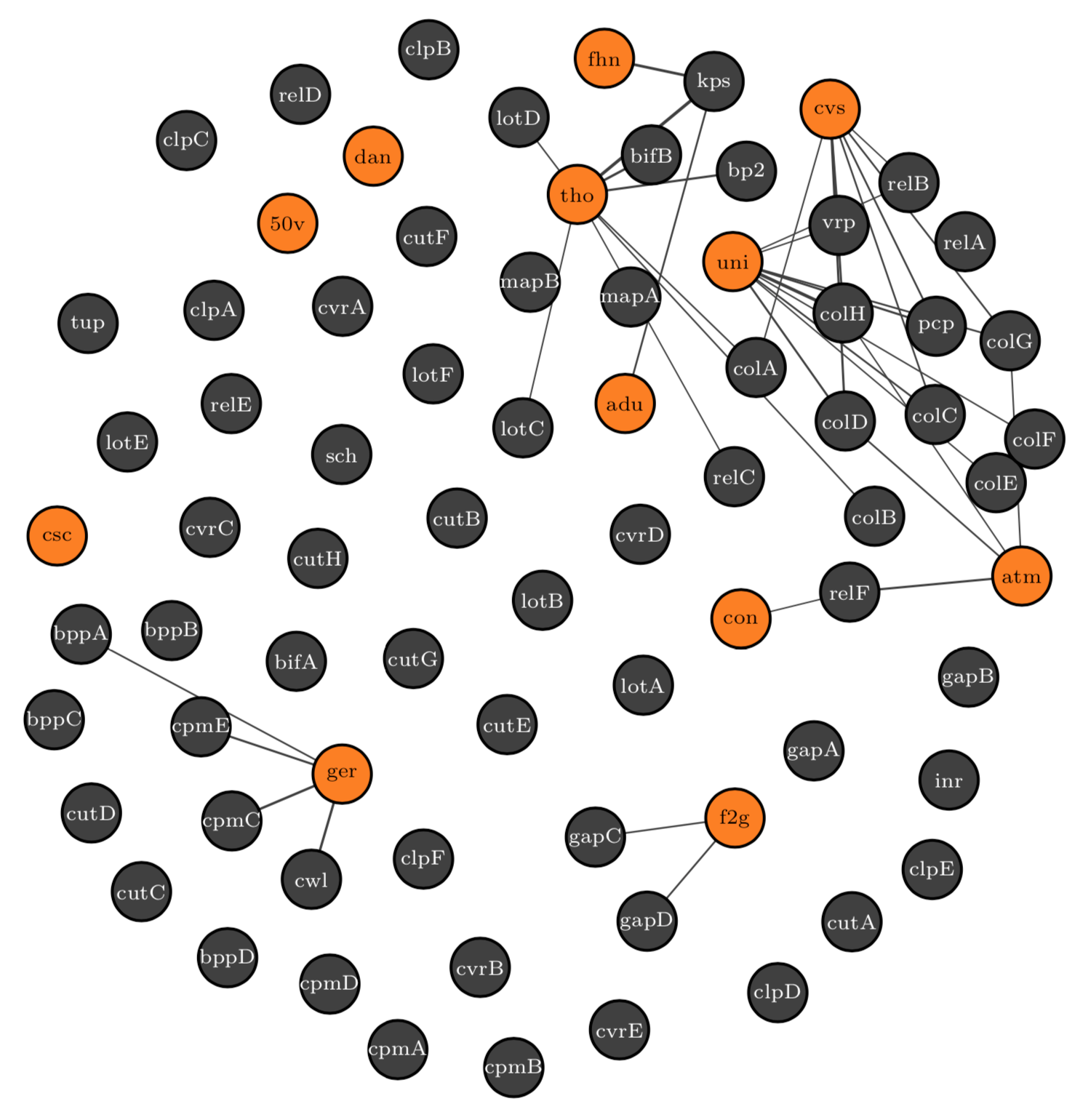
The data set for this analysis included a total of 950 MIP instances - 50 from each of 19 unique problem types. An autoencoder was trained on the corresponding set of CCM images, and subsequently used to generate 950 feature vectors. ISS values were computed between individual feature vectors, and also between average feature vectors at both the source and problem-type levels. The network visualizations below depict the relationships between pairs of problem types. Edges are drawn between problem pairs which share an ISS value below the defined threshold. Use the slider to change this threshold for yourself, and watch the connections grow! See the table below for problem descriptions.
Finally, we encourage others to study these instances on their own. There's no need to recreate our subset of strIPlib instances on your own, though. Click here to download the data set used in this analysis.
Network Visualizations
These are network visualizations of the relationships between strIPlib problem types.
  |
These are network visualizations of the relationships between strIPlib problem types.
|
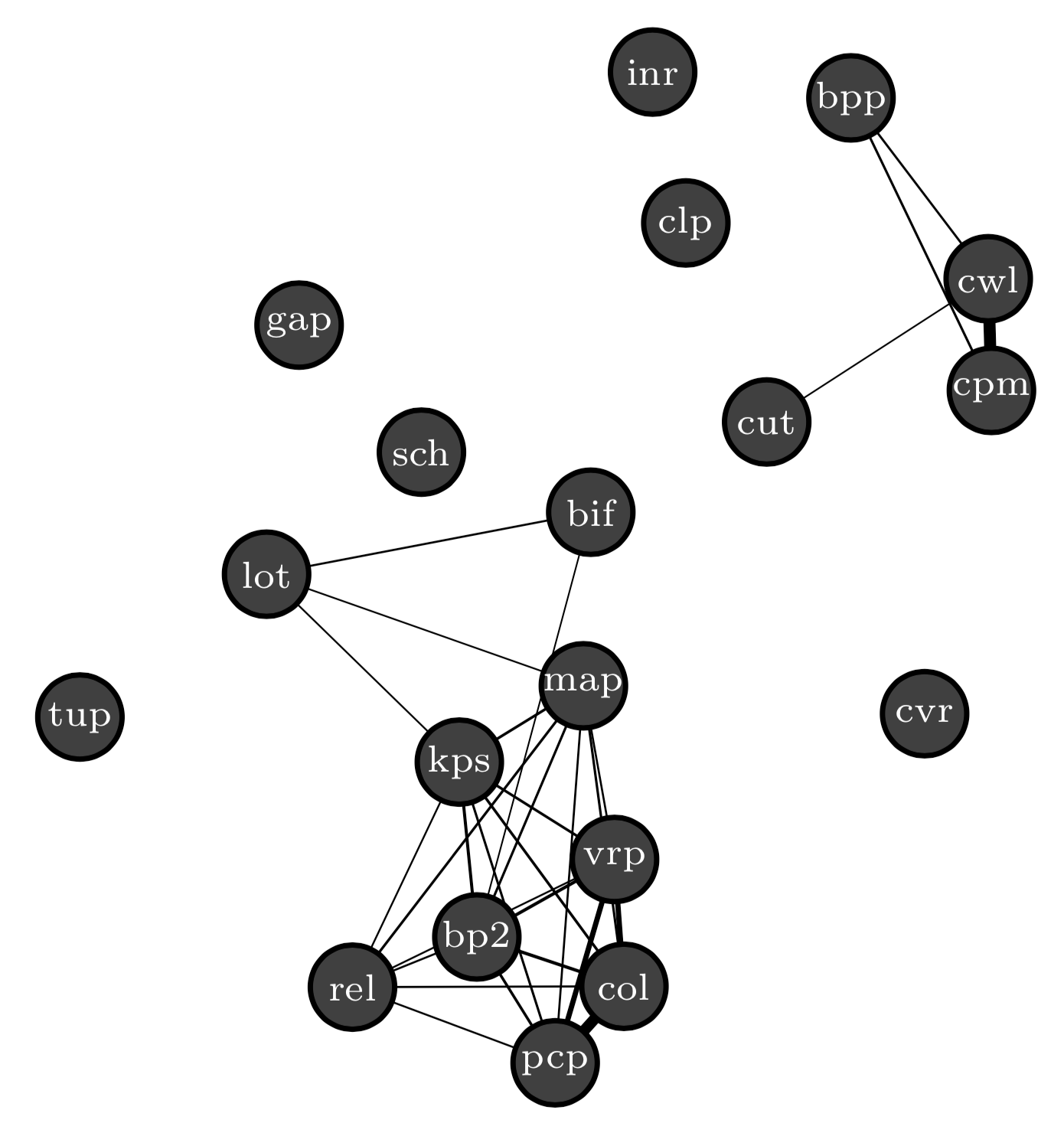 |
Problem types
This table contains problem descriptions and composite CCM images for each of the 19 strIPlib problem types considered in this study. Click on any problem abbreviation to see the corresponding results from SIP, as well as a list of all the submission sources for that problem type.
| ABBREVIATION | PROBLEM TITLE | COMPOSITE IMAGE |
|---|---|---|
| bpp | Bin packing problem |  |
| bp2 | Two-dimensional bin packing problem |  |
| bif | Bin packing problem with item fragmentation |  |
| clp | Container loading problem |  |
| col | Vertex coloring problem |  |
| cpm | Capacitated p-median problem |  |
| cut | Cutting stock problem |  |
| cvr | Capacitated vehicle routing problem |  |
| cwl | Capacitated warehouse (facility) location problem |  |
| gap | Generalized assignment problem |  |
| inr | International nurse rostering problem |  |
| kps | Knapsack problem with setups |  |
| lot | Lot sizing problem |  |
| map | Map labeling problem |  |
| pcp | Graph partition coloring problem |  |
| rel | Relaxed clique covering problem |  |
| sch | Scheduling problem |  |
| tup | Traveling umpire problem |  |
| vrp | Vehicle routing problem with time windows |  |